|
Chapter 4. 동력학적 분석 |
|
1. 동력학적분석 (1) 목표 1) 변형작용을 일으킨 응력에 대해 분석 (interpret the stresses that produce deformation) 2) 응력을 야기 시킨 힘의 성질에 대해 설명 (describe the nature of the forces from which the stresses are derived) 3) 응력, 변형 및 암석의 강도와의 상호관계에 대해 연구 (evaluate the overall relationships among stress, strain, and rock strength) 2. Force (힘) (1) 힘 1) 정의: 물체의 운동상태를 변화시킴 2) 뉴우톤의 제 1 운동법칙: 관성의 법칙 3) 뉴우톤의 제 2 운동법칙: F = ma (force = mass acceleration) (2) 질량 (Mass) 과 무게 (Weight) 1) 질량: 물체가 가지고 있는 물질의 양 (the amount of material the body contains) 2) 무게: 질량에 중력가속도가 작용하여 생긴 힘의 양 (the magnitude of the force of gravity acting on the mass) (3) 힘벡터: 크기와 방향 1) 정적평형 (static equilibrium): 회전력과 힘이 모두평형 2) 동적평형 (dynamic equlibrium): 회전 없이 일정한 속도로 직선을 따라 이동 (moving at a constant velocity in a straight line without spinning) (4) 힘의 종류 (Types of Forces) 1) 물체력 (body force): 물체의 모든 점에 작용 (act on each particle of mass, independent of the surrounding material). 2) 표면력 (surface force): 접촉면이나 물체 속에 존재하는 면에 작용(arise either from the action of one body on another across the surface of contact between them or from the action of one part of a body on another part across an internal surface). (5) 지질구조를 형성하는 힘 1) 중력 2) 열 대류에 의한 힘 3) 연성 변형환경에서의 물질이동 3. 응력 (Stress) (1) 개념의 발달 (Development of the Concept of Stress) 1) 힘 2) 힘세기 (Traction): 단위면적 당 작용하는 힘. 3) 응력 (Suface stress): 반대방향으로 작용하는 쌍의 힘세기. 4) 한 점에서의 응력 (Stress at a point): 한 점의 모든 방향에서 작용하는 응력.  (2) 응력 1) 단위면적에 작용하는 힘 . 2) 수직응력 (Normal stress (σ) : 평면에 수직으로 작용하는 응력 압축응력 (compressive stress): 수축에 대한 응력 (부호: +) 인장응력 (tensile stress): 신장에 대한 응력 (부호: -) 3) 전단응력(Shear stress (τ)) 면에 평행하게 작용하는 응력. 좌수향; 반시계방향 전단응력 (부호: -); 우수향; 시계방향 전단응력 (부호: +). 4. 정압응력 (Lithostatic Stress) (1)지각내에서의 응력 1) 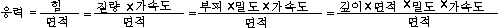 2)정압응력= 깊이×밀도×가속도(중력) 5. 평면에 작용하는 응력 계산 (1) 조그만 쐐기꼴 암석에서 힘의 평형 1) 힘=응력×면적 (2) 수평방향과 수직방향의 힘의 평형을 이용하여 1) 수평응력 (x축과 평행; Sx) 계산 2) 수직응력 (y축과 평행; Sy) 계산 (3) 평면에 작용하는 응력 (σxx)계산 (4) 평면에 작용하는 수직응력 (normal stress)와 전단응력 (shear stress) 계산 1) 수직응력: σN=σxzsinθ 2) 전단응력: σs=σxzcosθ 6. 응력텐서 (Stress Tensor) (1) 한 점의 모든 평면에 대한 응력 (2) 응력의 크기와 방향이 체계적으로 변화한다. (3) 주응력과 평행하거나 수직인 면에 작용하는 전단응력의 크기는 0이다. 7. 응력타원 (Stress Ellipse)과 응력타원체 (Stress Ellipsoid) (1) 응력타원 1) 주응력 (principal stresses): 전단응력이 0 인 면에 작용하는 수직응력 2) 주응력축 (axes of stress ellipse): 최대응력축 (axis of greatest principal stress(σ1)) 최소응력축 (axis of least principal stress(σ3)) (2) 응력타원체 1) 응력타원체의 축 (axes of stress ellipsoid) 최대응력축 (axis of greatest principal stress(σ1)) 중간응력축 (axis of intermediate principal stress(σ2)) 최소응력축 (axis of least principal stress(σ3)) 2) σ1, σ2, σ3 는 서로 직각이다. 8. 응력방정식 (1) 주응력에 대해 방향이 알려진 평면에 작용하는 수직응력과 전단응력을 계산하는 방정식 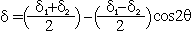 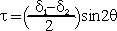 9. 모어응력그림 (The Mohr Circle of Stress (1) 주응력에 대해 방향이 알려진 평면에 작용하는 수직응력과 전단응력을 그림으로 표현하는 방법 (2) 모어응력그림 그리는 과정 1) x-축; 수직응력, y-축: 전단응력 2) x-축에서 주응력값 표시 3) 모어원의 중심을 찾아 원을 그린다. 4) x-축으로부터 2θ 측정한다. 5) 반경을 그린다. 6) 이 반경이 모어원과 만난 점의 수직응력과 전단응력 값을 읽는다. (3) 모어원 1) 평균응력 (mean stress): 모어원의 중심 2) 편차응력 (deviatoric stress): 모어원의 반경 3) 차응력 (differential stress): 모어원의 직경 (4) 응력이미지 (Images of Stress) 1) 정수압력 (hydrostatic stress): 세 개의 주응력의 크기가 같다. 모어응력 그림에서 점 2) 일축응력 (uniaxial stress): 두 개의 주응력의 값이 0이다. 3) 축응력 (axial stress): 두 개의 주응력의 값이 같다. 4) 삼축응력 (triaxial stress): 세 개의 주응력이 다르다. 10. 실험실에서의 변형작용 연구 (1) 유동학 (rheology): 주어진 응력에 대해 암석의 반응에 대해 연구 (2) 실험적 암석의 변형작용 연구: 지각 내에서의 물리적 환경하에서 응력과 변형과의 관계에 대해 연구 (3) 실험종류 1) 축신장실험 (axial extension) 2) 삼축압축실험 (triaxial deformation experiments) 3) 인장강도실험 (tensile strength tests) (4)변형률 (Strain Rate) 1)변형률= strain rate = 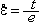 (5) 실험과정 1) 코어의 양끝을 잘 연마한다. 2) 코어의 직경과 길이를 측정한다. 3) 구리판으로 코어를 잘 감싼다. 4) 코어를 삼축압축실험기에 넣는다. 5) 균등압력을 준다. 온도, 공극압력, 변형률을 조절한다. 6) 축압력을 가한다. 7) 응력을 계산한다. 8) 변형을 측정한다. (6) 축압축실험 1) 응력-변형그림 (stress-strain diagram) ① y-축: 차등응력 (differential stress); ② x-축: 변형 2) 탄성변형작용 (elastic deformation): 응력을 제거했을 때 암석이 원래상태로 돌아간다. 3) 소성변형작용 (plastic deformation): 모양변화를 일으킨다. 4) 탄성한계 (elastic limit): 응력-변형그림에서 탄성변형작용에서 소성변형작용으로 변하는 곳 5) 항복강도 (yield strength): 탄성한계에서의 차등응력 값 6) 변형경화 (strain hardening): 소성변형작용에 의해 항복강도가 증가하는 현상 7) 변형연화 (strain softening): 부가 변형을 일으킬 때 응력이 덜 드는 현상 8) 극한강도 (ultimate strength): 응력-변형그림에서의 최고점의 차등응력 9) 파열강도 (rupture strength): 단층이 발달하였을 때의 차등응력 (7) 암석강도와 연성도(Strength and Ductillity) 1) 암상 ① 약한강도: 암염, 경석고, 셰일, 이암 ② 중간강도: 석회암, 방해석으로 교결된 사암 ③ 강한 강도: 규암, 화강암, 석영으로 교결된 사암 ④ 연약한 (incompetent)암석: 연성변형작용에 의해 변형됨 ⑤ 강한 (competent)암석: 취성변형작용에 의해 변형됨 2) 균등압력과 공극암 (Confining Pressure and Pore Fluid Pressure ① 균등압력의 증가: 암석 강도와 연성도를 증가 ② 공극압의 증가: 암석 강도와 연성도를 감소 ③ 유효응력: 균등압력 - 공극압 3) 온도 ① 온도증가: 항복강도 및 극한강도 감소, 연성도 증가 4) 변형률 ① 일차포행 (primary creep): 시간이 지남에 따라 변형이 감소, 변형률 감소 ② 이차포행 (secondary creep): 시간이 지남에 따라 일정하게 변형이 증가, 변형률 일정 ③ 삼차포행 (tertiary creep): 시간이 지남에 따라 변형이 증가. 변형률 증가 11. 탄성, 소성, 점성 변형 (1) 탄성변형 1) 변형과 응력 그림에서 일차적인 관계 (linear relationship) 후크의 법칙σ=Ee 2) 영률: E, 변형-응력 그림에서 기울기, 단단함 (stiffness)을 나타남 3) 프와송비 (Poisson's ratio):ν, 신장변형과 측면변형의 비 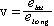 4) 전단율 (shear modulus): G τ= G·γ 5) 체적탄성률 (bulk modulus): K 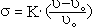 6) 압축률 (compressibility):1/K (2) 소성변형 1) 극복되지 않는(영원한) 변형 2) 항복강도 이전에는 변형이 일어나지 않으나 항복강도를 극복한 이후에는 응력이 없어질 때까지 변형이 계속됨 (3) 점성변형 1) 모든 응력에 대해 변형이 발생 2) 항복강도가 없음 3) 점성도: 유동에 대한 저항 4) 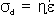 where σd = differential stress η= viscosity 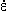 = strain rate = strain rate (4) 점성- 탄성 변형 1) 점성과 탄성을 병렬로 연결 2) 응력을 제거했을 때 암석이 원래상태로 돌아가나, 변형축적이나 변형회복이 지체됨 3) σ=E·e + 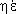 (5) 탄성-점성 변형 1) 탄성과 점성을 직렬로 연결 2) 처음에는 탄성변형 후에 점성변형이 일어남 3) 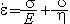 (6) 선변형 (Linear Behavior) 1) 점성-탄성과 탄성-점성 변형을 직렬로 연결 (7) 비선형 변형 (Nonlinear Behavior) 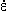 = σn·exp(-E = σn·exp(-EE*: activation energy R: 기체상수 T: 켈빈온도 |
| 처음으로 |





