1. 운동학적 분석
(1) 운동학적 분석: 변형작용 동안에 발생한 운동 (movements)에 대해 분석(그림 2.1)
(2) 변형작용
1) 강체변형작용 (rigid body deformation:그림 2.2)
① 병진운동 (translation: 그림 2.2)
② 회전운동 (rotation:그림 2.3)
③ 강체 내부의 각 점은 상대적인 운동이 없다(그림 2.6)
2) 비강체변형작용 (non-rigid body deformation: 그림 2.2)
① 체적변화 (dilation: 교과서 그림 2.4)
② 변모 (distortion: 교과서 그림 2.5)
③ 변형 (strain): 체적변화 + 변모
④ 비강체 내부의 각 점은 상대적인 운동이 있다(그림 2.6)
2. 병진운동
(1) 병진운동
1) 순수병진운동: 물체의 모든 점이 평행하게 이동(그림 2.7)
2) 지질구조: 절리, 단층, 맥(그림 2.8, 2.9, 2.10)
(2) 변위벡타 (Displacement vector)
1) 세 개의 제한요소(parameters)를 이용하여 기술(그림 2.11, 2.12, 2.13, 2.14, 2.15, 2.16, 2.17, 2.18, 2.19)
2) 제한요소
① 이동거리 (Distance of transport): 예, 90 cm
② 이동방향 (Direction of transport): 선주향 과 선경사. 예, N30oW
③ 운동감각 (Sense of transport): 예, 북서 쪽으로
3. 회전운동
(1) 회전운동(그림 2.20, 2.21, 2.22, 2.23, 2.24)
1) 세 개의 제한요소(parameters)를 이용하여 기술
2) 제한요소
① 회전축(axis of rotation): 선경사 와 선주향
② 회전방향 (Sense of rotation): 시계방향 또는 반시계방향
③ 회전각 (magnitude of rotation): 각도로 표시. 예, 50。
3) 지질구조: 단사구조, 곡면정단층(listric normal fault), 아프리카 대륙, 회전된 석류석
4. 변형(Strain)
(1) 변형
1) 변형: 체적변화 와 변모
2) 체적변화: 물체 속의 두 점간의 거리가 멀어지거나 가까워짐
3) 변모: 물체 속의 두 점간의 거리가 변하나 일부는 변하지 않음
(2) 변형타원(Strain ellipse: 그림 2.25, 2.26, 2.27, 2.28)
1) 변형타원: 변형작용에 의해 물체 속의 상상의 원이 변해서 된 타원
2) 무한소변형타원(Infinitesimal strain ellipse): 아주 작은 변형을 나타내는 타원, 거의 원에 가깝다.
3) 유한변형타원(finite strain ellipse): 변형작용에 의해 물체 속의 상상의 원이 변해서 최종적으로 형성된 타원
(3) 길이의 변화 (그림 2.29, 2.30, 2.31, 2.32, 2.33)
1) 신장(Extensioin, Elongation): 단위길이의 변화
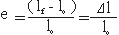
2) 스트레치(Stretch): 변형 전과 후의 길이의 비
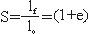
3) 이차신장(Quadratic elongation): 스트레치의 제곱
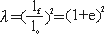
4) 자연변형(Natural strain, logarithmic strain): 점진적인 신장 변형작용의 합

(4) Skolithus burrow(그림 2.34)를 이용한 길이의 변화 결정
1) 원래의 원의 면적 vs. 타원의 면적
2) 원래의 원의 반경(r=1.2)
3) 변형 제한요소(파라미터) 결정
(5) 각의 변화(그림 2.36, 2.37)
1) 각전단(Angular shear): 변형전 직각이던 직선들의 각의 변화 ( ψ)
① 부호: 시계방향: + , 반시계방향: -
② 회전양: 각도
2) 전단변형(Shear strain): 각전단의 탄젠트(그림 2.38, 2.39)
① 부호: 시계방향: + , 반시계방향: -
② γ=tanψ
(6) 균질변형(Homogeneous strain) 과 비균질변형(Inhomogeneous strain)
1) 균질변형(그림 2.39, 2.40)
① 직선들은 변형작용 후에 직선으로 남는다.
② 평행선들은 변형작용 후에 평행하다.
③ 변형작용 후에 어느 한 방향에 대해 모든 변형파라미터들이 일정하다(e, λ, ψ, γ
).
2) 불균질 변형
① 직선들은 변형작용 후에 곡선이 된다.
② 평행선들은 변형작용 후에 평행하지 않다.
③ 변형작용 후에 어느 한 방향에 대해 모든 변형파라미터들이 변화한다(e, λ, ψ, γ
).
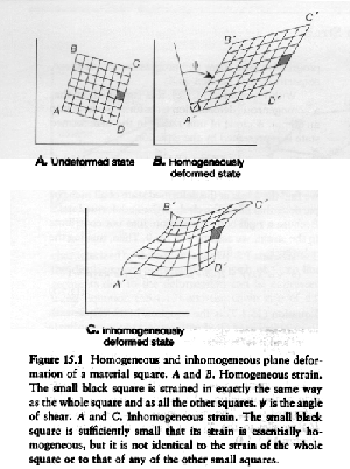
(7) 유한변형타원(finite strain ellipse: 그림 2.41, 2.42, 2.43, 2.44)
1) 암석의 변형을 기하학적으로 나타낸 방법
2) 유한변형타원의 주축(principal axes)
① 장축: 최대 유한 스트레치, 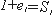
② 단축: 최소 유한 스트레치, 
③ 주축들의 각전단의 값은 0 이다.
3) 타원율(ellipticity)
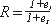
(8) 변형방정식(그림 2.45)
1) 역이차신장(reciprocal quadratic elongation)
①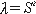
②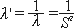
2) 변형방정식
①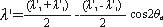
②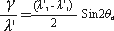
(9) 유한변형타원에서의 변형계산 (그림 2.46)
1) 주축은 최대신장과 최소신장 이며 전단변형은 0 이다.
2) 스트레치가 1인 방향 두 개가 존재(no finite stretch)
3) 전단변형이 최대인 방향이 두 개 존재
4) 스트레치와 전단변형이 방향에 따라 규칙적으로 변화한다.
(10) 모어 변형그림(The Mohr Strain Diagram: 그림 2.47, 2.48, 2.49, 2.50, 2.51)
1) 변형방정식을 그래프에 표현
2) x-축: 역이차신장, y-축: 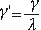
3) 원의 중심: 변형방정식의 첫째 term
4) 원의 반경: 변형방정식의 둘째 term의 처음부분
5) 모든 방향의 역이차신장값과 전단변형값을 구할 수 있다.
6) 모어변형 그림을 이용하기 위하여 필요한 자료
① 선(방향)의 에 대한 방향
② S 1 과S 2
(11) 변형타원체(그림 2.52, 2.53)
1) 구가 변형작용을 받아 형성된 타원체
2) 구방정식: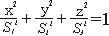
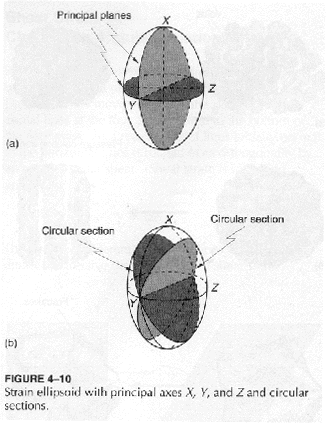
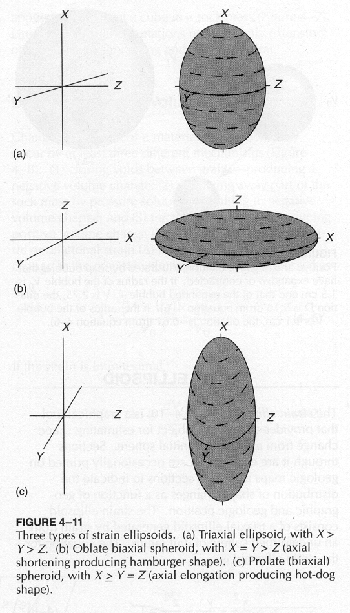
3) 변형타원체의 형태
① 삼축타원체(triaxial ellipsoid)
② 편원타원체(oblate biaxial spheroid)
③ 편장타원체(prolate biaxial spheroid)
(12) 변형타원체의 모양(The Representation of Strain States: Flinn diagram)
1) 축: 절대적인 변형량을 구하는 것이 아니라 상대적인 양의 비를 계산
x 축: 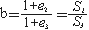
y 축: 
2) k 값: 변형타원체의 크기가 아니라 형태(shape)를 나타냄
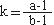
0  k < 1: 편평변형(flattening strain) k < 1: 편평변형(flattening strain)
k = 1: 평면변형(plane strain)
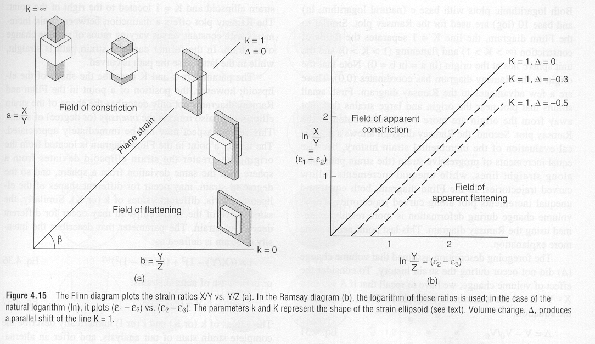
1 < k < 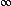 : 수축변형(constrictional strain) : 수축변형(constrictional strain)
(13) 부피변화(그림 2.54, 2.55, 2.56, 2.57)
1) 변형영역그림 (strain field diagram: 그림 2.58)
① 팽창영역(field of expansion)
② 수축영역(field of contraction)
③ 보존영역(field of compensation)
④ 단축영역(field of linear shortening)
⑤ 신장영역(field of linear stretching)
⑥ 무변형영역(field of no strain)
2) 체적변형(Volumetric strain)
① 체적팽창(volumetric extension = Δ(dilation))
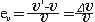
(14) 순수전단과 단순전단(그림 2.59)
1) 평면변형 형태
2) 순수전단: 동축변형(coaxial deformation)
① 주변형축이 변형이 진행되는 동안 변하지 않는다.
② 한 방향으로 수축변형이 일어나고 그와 직각방향으로 신장변형이 일어난다.
3) 단순전단: 비동축변형(noncoaxial deformation)
① 주변형축이 변형이 진행되는 동안 회전한다.
② 단순전단이 일어나는 암석밖의 암석들은 길이가 변하지 않는다.

(15) 변형의 형태(types)

|
|